Accurate determination of the number of sections of a bimetallic radiator capable of effectively heating a square meter of room area ultimately affects the overall economic effect of the heating system of an apartment or private house as a whole. A bimetallic battery consists of several elements, each of which is a steel pipeline enclosed in an aluminum casing.
The average heat transfer of the bimetal segment is about 160 – 180 W (datasheet). This value is taken as the initial parameter for preliminary calculation of the number of sections of a bimetallic radiator. To heat a room measuring 10 square meters, a radiator power of 1360 W is required.
The number of sections of a bimetallic battery is calculated by simply dividing the above two values: 1360/180 = 7.55 pieces. The result is rounded up, therefore it will take 8 segments to heat this room.
Currently, manufacturers and distributors of water heating heating devices, meeting the buyer halfway, publish online calculators on the Internet. The service allows the consumer, without going into calculations, in a couple of clicks to obtain the required number of sections in addition to the bimetallic battery, but also how many of them will be needed to assemble cast iron or aluminum radiators, and also find out the size of the steel panel appliance. A convenient online calculator for calculating the number of sections is presented in the next chapter.
Why is it dangerous to approximate the number of radiator sections?
The above method is quite approximate and does not take into account a lot of factors that influence the calculation result. The rated power of one element of an aluminum or bimetallic battery is quite relative. After all, its value can be obtained under certain conditions, where the heating temperature of the bimetal fin is 1000C, the ceiling height is up to 3 meters, there are no cold (external) walls in the room and there is only one window.
It seemed quite simple to calculate bimetallic heating radiators for an apartment with ceilings no higher than 2.7 m. It is enough to multiply the standard thermal power (136 W) of one bimetal segment by the number of meter squares in each room. The result is divided by the thermal power of one segment, the value of which is declared by the manufacturer. But therein lies the danger of making rough estimates.
Relying only on passport data and not taking into account the characteristics of the room, you can incorrectly calculate how many radiator sections are needed per 1 m2. This can lead to insufficient heating of the room or, on the contrary, force the excess heat to be removed by forced ventilation of the room. For an accurate calculation, you need to take into account all the nuances of the room conditions.
How to adjust preliminary indicators
Approximate values definitely need clarification. To obtain a more accurate result, you will need to take into account all factors.
Each of them can provoke an increase or decrease in heat loss:
- Material for walls.
- Thermal insulation efficiency.
- Area of window units and type of glazing.
- Number of external walls.

High-quality calculators are equipped with special coefficients that take these factors into account. All that is required to more accurately align the preliminary heat loss indicators is to multiply them by these coefficients.
Necessary data for calculation
As a rule, the accompanying documentation indicates the maximum heat transfer of one bimetallic segment - this averages 180 W under optimal heating conditions, while the accompanying heat loss must be taken into account due to the local characteristics of the room.
In the calculation that determines the number of sections, reduction factors are used.
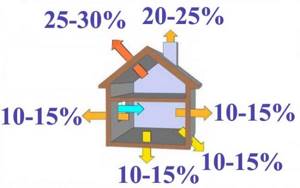
- Heat loss from the roof is 25 - 30%.
- Windows 10 – 15%.
- Paul 10 – 15%.
- Walls 10 – 15%.
- Adjacencies 10 – 15%.
- Pipe (if any) 20 - 25%.
Calculation of heating radiators by area
The easiest way. Calculate the amount of heat required for heating, based on the area of the room in which the radiators will be installed. You know the area of each room, and the heat requirement can be determined according to SNiP building codes:
- for an average climate zone, heating 1 m2 of living space requires 60-100 W;
- for areas above 60° 150-200W is required.
Based on these standards, you can calculate how much heat your room will require. If the apartment/house is located in the middle climate zone, heating an area of 16 m2 will require 1600 W of heat (16*100=1600). Since the standards are average, and the weather is not constant, we believe that 100W is required. Although, if you live in the south of the middle climate zone and your winters are mild, count 60W.

Calculation of heating radiators can be done according to SNiP standards
A power reserve in heating is needed, but not very large: with an increase in the amount of power required, the number of radiators increases. And the more radiators, the more coolant in the system. If for those who are connected to central heating this is not critical, then for those who have or are planning individual heating, a large volume of the system means large (extra) costs for heating the coolant and greater inertia of the system (the set temperature is less accurately maintained). And a logical question arises: “Why pay more?”
Having calculated the room's heat requirement, we can find out how many sections are required. Each heating device can produce a certain amount of heat, which is indicated in the passport. Take the found heat requirement and divide it by the radiator power. The result is the required number of sections to make up for losses.
Let's count the number of radiators for the same room. We determined that 1600W needed to be allocated. Let the power of one section be 170W. It turns out 1600/170 = 9.411 pieces. You can round up or down at your discretion. You can turn it into a smaller one, for example, in the kitchen - there are plenty of additional heat sources there, and a larger one - better in a room with a balcony, a large window or in a corner room.
The system is simple, but the disadvantages are obvious: ceiling heights can be different, wall material, windows, insulation and a number of other factors are not taken into account. So the calculation of the number of sections of heating radiators according to SNiP is approximate. For an accurate result, you need to make adjustments.
Heat loss coefficients
For the design of heat supply systems, a Code of Rules was developed and approved based on SNiPs GOST 30494-2011 and GOST 32415-2013. SP 60.13330.2016 regulates the rate of supply of thermal power in the amount of 1 kW for a room of 10 sq.m., with a ceiling height of up to 3 meters, one external (cold) wall and one window.
To bring the initial data into line with the actual operating conditions of the joint venture heating battery, the following coefficients were developed to correct heat loss.
K1 – takes into account the structure of the frames:
- double window frames – 1.27;
- double glazing of fiberglass windows – 1.0;
- triple – 0.85.
K 2 – takes into account the thickness of the walls:
- wall of 1 brick – 1.27;
- brickwork of 2 bricks – 1;
- high degree of thermal insulation - 0.85.
К 3 – ratio of window area to floor area:
- 1/2 – 1,2;
- 1/3 – 1,0;
- 1/10 – 0,8.
K 4 – average indoor air temperature in winter:
- 30 degrees – 1.5;
- 20 – 1,1;
- 10 – 0,7.
K 5 – number of cold vertical fences:
- 1 – 1,1;
- 2 – 1,2;
- 3 – 1,3;
- 4 – 1,4.
K 6 – space above the room:
- Cold under-roof volume – 1.0;
- attic or residential floor of an apartment building - 0.8.
K 7 – ceiling height:
- 2500 mm – 1.0;
- 3000 mm – 1.05;
- 3500 mm – 1.1.
After entering the correction factors into the calculation, the resulting total is divided by the heat transfer of one section. The number of sections is rounded up to the nearest whole number. For example, if it turns out to be 10.4, then 11 sections are accepted.
Another calculation example
A room with an area of 15 m2 and a ceiling height of 3 m is taken as an example. The volume of the room is calculated: 15 x 3 = 45 m3. It is known that to heat a room in an area with an average climate you need 41 W/1 m3.
45 x 41 = 1845 W.
The principle is the same as in the previous example, but heat transfer losses due to windows and doors are not taken into account, which creates a certain percentage of error. To make a correct calculation, you need to know how much heat each section produces. Steel panel batteries can have fins in different numbers: from 1 to 3. The number of fins a battery has, the greater the heat transfer.
https://youtube.com/watch?v=ZkvOaJlQetM
The greater the heat transfer from the heating system, the better.
Calculation methodology
It is used to determine the actual temperature difference Δt (the difference between the average temperatures of the coolant in the radiator and the air in the room). The calculation is made according to the formula:
Δt = (tflow + treturn)/2 – tair
Taking into account the standard Δt = 700 C and the average air temperature in the room - 220 C, we obtain:
(tfeed + treturn) = 2(70 + 22) = 1840 C
Taking into account that the basic standard for the temperature difference between supply and return is 200 C, their value is determined:
tfeed = (184 + 20)/2 = 1020 C
treturn = (184 – 20)/2= 820 C
In reality, this is simply impossible. The fact is that the boiler can produce maximum water heating of no more than 800 C, and a maximum of 770 C will reach the heating battery. Δt will be approximately 400 C. Consequently, the real heat transfer of the 1st section will not be 180 W, but 100 W. To simplify the calculation of heat transfer, a table of reduction factors is used.
| Δt | TO |
| 40 | 0,48 |
| 45 | 0,56 |
| 50 | 0,65 |
| 55 | 0,73 |
| 60 | 0,82 |
| 65 | 0,91 |
| 70 | 1 |
The rated power value is multiplied by the corresponding coefficient. That is, heating one square meter of room area will require a heat transfer of 180 x 0.48 = 86.4 W. Rounding up, it turns out that heating 10 m2 will require approximately 1 kW of heat transfer. That is, dividing 1 kW by 86.4 W, we get 1000/86.4 = 9 sections.
When the ceiling height is more than 2.5 m, the calculation is made taking into account the volume of the room. To do this, factor K7 is introduced into the calculation (see the heat loss coefficients chapter above).
Parameters influencing the calculation result
As already mentioned, the heat transfer rating of one element, declared by the manufacturer in the attached product passport, is calculated for optimal room conditions. From here, the standard number of required battery segments is established so that one square meter of room can be fully heated.
Calculation of radiator sections. How to calculate sections in a heating radiator. Battery.
Rooms, both in an apartment and a private house, have their own specific heating conditions. Room parameters may differ significantly from standard values.
An effective and professionally accurate calculation of the number of heating elements in bimetallic batteries can only be carried out by heating specialists. When calculating, they take into account a large number of parameters that affect the final result of the research.
In order not to bore the reader with the specific subtleties of a professional approach in this matter, we will focus on the basic data necessary for accurately calculating the segments of bimetallic heating radiators - these are:
- the material from which the walls are built;
- thickness of enclosing structures;
- average ambient temperature in winter;
- type of window frames (double wooden frames, double or triple glazing);
- the presence of a heated or cold room above the room;
- number of cold barriers;
- room area;
- ceiling height.
A correction factor is selected for each parameter. The 7 most commonly used coefficients are listed above.
Calculation of the number of bimetallic sections per 18 m2
To make it clearer how the whole process of selecting the number of sections in the battery occurs, you can consider the calculation, for example, for a room with an area of 18 m2. Initially, choose the room heating conditions that are most often encountered in practice:
- bimetallic radiator model;
- connection type;
- finding a room;
- determination of thermal pressure;
- room conditions;
- calculation of heat transfer of the bimetallic section;
- calculation of the total number of sections per 18 m2.
Bimetallic radiator model
Let’s say a hypothetical buyer has chosen a sectional bimetallic radiator of the ATLANT Eco 500/96 brand. The number 500 means the center-to-center distance between the centers of the sections of the upper and lower collector. Bimetallic batteries also come with a distance between the axes of the collectors of 350 mm.

In the characteristics of this model, the manufacturer indicated the power of one section is 160 W with a thermal pressure Δt = 700C. One segment is designed to heat 1.8 m2. These passport data will need to be adjusted to the actual heating conditions of the room.
Connection type
Radiators can be either with one-sided or two-sided pipe connections.
Double-sided connection of radiators
One-sided connection of radiators
In this case, the radiator is selected with two-way pipe connections, with the coolant inlet located at the top, and the return flow exits through the lower hole.
Room location
The room can be one of the rooms of a private house or apartment. It is also important what is located above the room: the heated or cold space of the house or apartment.
In this case, choose a room in an apartment with a residential upper floor.
Determination of thermal pressure
The previous chapter “Calculation Methodology” provides an example of calculating the actual thermal pressure. In the present case, the thermal pressure will be equal to 700 C.
According to the table, the corresponding coefficient is 1.0.
Premises conditions
The previous chapter “Heat loss coefficients” lists room conditions that can significantly affect the design power of a bimetallic radiator. As an example, select the average data and the values of the corresponding coefficients:
- the ceiling height is taken to be 3 m (1.05);
- the space above the room is the residential floor (0.8);
- number of cold (outer walls) – 1 (1.1);
- the average temperature in the room in winter is 200 C (1.1);
- ratio of window and floor areas – 1:3 (1.0);
- thermal insulation of walls - masonry of 2 bricks (1.0);
- structure of window frames – double glazing (1).
Calculation of thermal power of the 1st bimetallic element
The power of one heating element of the ATLANT Eco 500/96 radiator, specified by the manufacturer, is 160 W. Thermal pressure coefficient is 1.0, which does not change the original value - 160 W. Using all heat loss coefficients, the final calculation of the heat transfer of the 1st section is made.
160 W x K-1 x K-2 x K-3 x K-4 x K-5 x K-6 x K-7 = 160 x 1.05 x 0.8 x 1.1 x 1.1 x 1 .0 x 1.0 x 1.0 = 160 x 1.0164 = 162 W.
Calculation of the total number of sections per 18 m2
Calculation of heating radiators Part 1
Calculations have confirmed that one bimetallic section will heat 1.8 m2 of room area, maintaining the average air temperature in winter within 200 C.
Therefore, to heat a room with an area of 18 m2, you will need an ATLANT Eco 500/96 battery, consisting of ten sections.
Approximate calculation for standard premises
A very simple calculation option. It is based on the fact that the size of mass-produced heating batteries is practically the same. If the room height is 250 cm (standard for most living spaces), then one radiator section can heat 1.8 m2 of space.
The area of the room is 14 m2. To calculate, it is enough to divide the area value by the previously mentioned 1.8 m2. The result is 7.8. Round up to 8.
Thus, to warm up a 14-meter room with a 2.5-meter ceiling, you need to buy a battery with 8 sections.
Important! Do not use this method when calculating a low-power unit (up to 60 W). The error will be too large.
How to assemble a sectional radiator with your own hands
You may not be able to find a segment battery with the required number of sections on sale. Then there is the opportunity to purchase individual sections and assemble them together with your own hands.

Their advantage is that the homeowner can always increase or decrease the heat transfer of the batteries by adding or dismantling sections. Along with the segments, fittings (nipples with external threads), O-rings and connecting pipes are purchased.
Assembly is carried out with a special key. Since the sectional design has many connecting points, poor-quality assembly of the radiator can cause leaks at the junctions of the sections. Therefore, you need to screw the segments into one structure very carefully.
Why do you need to calculate the number of sections of heating batteries?
It is impossible to accurately count bimetallic sections without correctly forming a base of initial data. It is necessary to determine the volume of heat loss in the room, make the right choice of the battery manufacturer, find out the temperature of the coolant at the inlet and outlet of the radiator, and also determine the comfortable temperature in the room.
Based on these indicators, it is possible to calculate with complete confidence the number of sections of a bimetallic radiator for heating 1 m2 of room area. Correct calculation of the number of segments in one radiator will significantly reduce heating costs.
The sectional structure of heating devices allows you to select the required number of sections in an existing residential heating system by dismantling them or, conversely, installing additional segments.
How many radiator sections are needed per square meter?
Calculation of different types of radiators
If you are planning to install sectional radiators of a standard size (with an axial distance of 50 cm in height) and have already chosen the material, model and desired size, there should not be any difficulties in calculating their number. Most reputable companies that supply good heating equipment have on their website the technical data of all modifications, including thermal power. If it is not the power that is indicated, but the coolant flow rate, then it is easy to convert to power: the coolant flow rate of 1 l/min is approximately equal to the power of 1 kW (1000 W).
The axial distance of the radiator is determined by the height between the centers of the holes for supplying/removing coolant.
To make life easier for customers, many websites install a specially designed calculator program. Then the calculation of heating radiator sections comes down to entering data on your premises in the appropriate fields. And at the output you have the finished result: the number of sections of this model in pieces.

The axial distance is determined between the centers of the coolant holes
But if you’re just evaluating possible options, then it’s worth considering that radiators of the same size made of different materials have different thermal power. The method for calculating the number of sections of bimetallic radiators is no different from calculating aluminum, steel or cast iron. Only the thermal power of one section can be different.
To make it easier to calculate, there are averaged data that you can use as a guide. For one radiator section with an axial distance of 50 cm, the following power values are accepted:
- aluminum - 190W
- bimetallic - 185W
- cast iron - 145W.
If you are just figuring out which material to choose, you can use this data. For clarity, we present the simplest calculation of sections of bimetallic heating radiators, which takes into account only the area of the room.
When determining the number of heating devices made of bimetal of a standard size (center distance 50 cm), it is assumed that one section can heat 1.8 m2 of area. Then for a room of 16 m2 you need: 16 m2/1.8 m2 = 8.88 pcs. Let's round up - we need 9 sections.
We calculate similarly for cast iron or steel bars. All you need is the following rules:
- bimetallic radiator - 1.8m2
- aluminum - 1.9-2.0 m2
- cast iron - 1.4-1.5 m2.
This data is for sections with an interaxial distance of 50 cm. Today, there are models on sale with very different heights: from 60cm to 20cm and even lower. Models 20cm and below are called curb. Naturally, their power differs from the specified standard, and if you plan to use a “non-standard”, you will have to make adjustments. Either look for passport data, or do the math yourself. We proceed from the fact that the heat transfer of a heating device directly depends on its area. As the height decreases, the area of the device decreases, and, therefore, the power decreases proportionally. That is, you need to find the ratio of the heights of the selected radiator with the standard, and then use this coefficient to correct the result.

Calculation of cast iron heating radiators. Can be calculated by area or volume of the room
For clarity, we will calculate aluminum radiators by area. The room is the same: 16m2. We count the number of sections of standard size: 16m2/2m2=8pcs. But we want to use small sections with a height of 40 cm. We find the ratio of radiators of the selected size to standard ones: 50cm/40cm=1.25. And now we adjust the quantity: 8pcs * 1.25 = 10pcs.